受験指導を担う塾講師にとって、定期テストや模擬試験の成績データを正しく読み解く能力が重要であることは言うまでもありません。特に、模試の結果が悪かった際には、それまでの指導を継続して良いのか方針を見直すべきなのかの判断を誤ってしまうと、更にその後も成績を落とすことになりかねません。

データの正確な読み取りには統計学の知識が欠かせません。なぜなら、同じデータでも直感的な解釈と統計的な解釈では、真逆の結論になることが珍しくないからです。

統計的な知識を持って正しくデータを読み解けるようになると、毎回の模試の結果に振り回されることなく、一貫した態度で指導に向かえるようになります。必然的に指導の成果も出やすくなります。少なくとも、模試の結果に生徒と一緒に一喜一憂し、成績が出るたびに指導方針が変わるようなことはなくなります。

そこで今回の記事では、難関校の受験指導を担うプロの講師として、生徒の成績データを読み解く上で重要な統計的知識を解説します。そのうえで、実際にどのような観点からデータを読んでいるのか、その考え方の一部をご紹介したいと思います。

統計がわかるとデータの見方が変わる

冒頭で「同じデータでも直感的な解釈と統計的な解釈では、真逆の結論になることすら珍しくない」と申しました。まずはその具体例を参照しながら、直感と相反する統計の世界を体感していただきます。

入塾直後に成績が下がったAさん

１つ目の具体例として、次のようなケースを考えてみましょう。

高校受験を控え、中学２年生の春から塾に通い始めたAさん。入塾直前に受けた模試の偏差値は53で、塾に通ってさらに成績を上げたいと考えていた。ところが、次に受けた夏の模試では偏差値が48となり、期待に反して悪い結果となってしまった。この結果を受けて保護者は「この塾はうちの子に合わないのでは」と思い、転塾を考え始めた。

このケースで考えていただきたいことがあります。それは、Aさんの成績が下がった理由です。なぜAさんは偏差値53から48へと成績を落としてしまったのでしょうか。

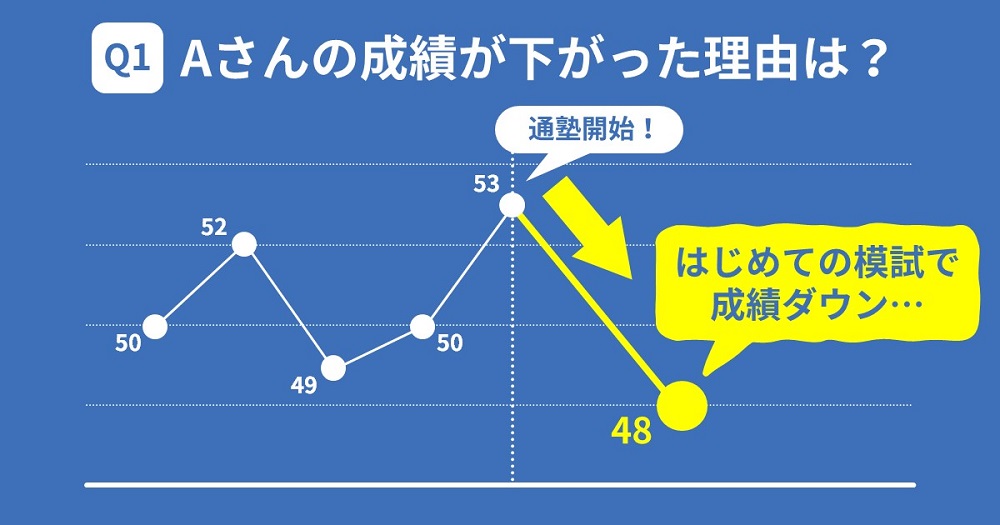
成績が下がった理由として、Aさんの保護者のように「塾の指導が合わなかった」と考えたい気持ちもわかります。しかし、統計的視点から今回のケースを評価すれば、模試の結果が悪かったのは「誤差の範囲内」と考えるのが妥当でしょう。

つまり、Aさんの学力はまだ上がっても下がってもおらず、単に調子が少し良かった前回と、調子が少し悪かった今回とが連続しただけだと考えられます（追って詳しく解説します）。

３回連続で成績が上がったBさん

続いて２つ目の例をみてみましょう。

入塾以来、コツコツと勉強を頑張ってきたBさん。入塾時から６年生になるまでは一貫して偏差値50前後をキープしていたが、６年生になってから成績向上の兆しが。毎月の月例テストで４月…48、５月…50、６月…52、７月…54と、５月以降３回連続で偏差値が２ずつ上がっている。

さて、ここで問題です。Bさんがこの次に受ける８月の月例テストの結果を予測してください。

７月の結果を基準に、「A…良くなる」「B…変化なし」「C…悪くなる」の３つの選択肢からどれか１つを選んでください。

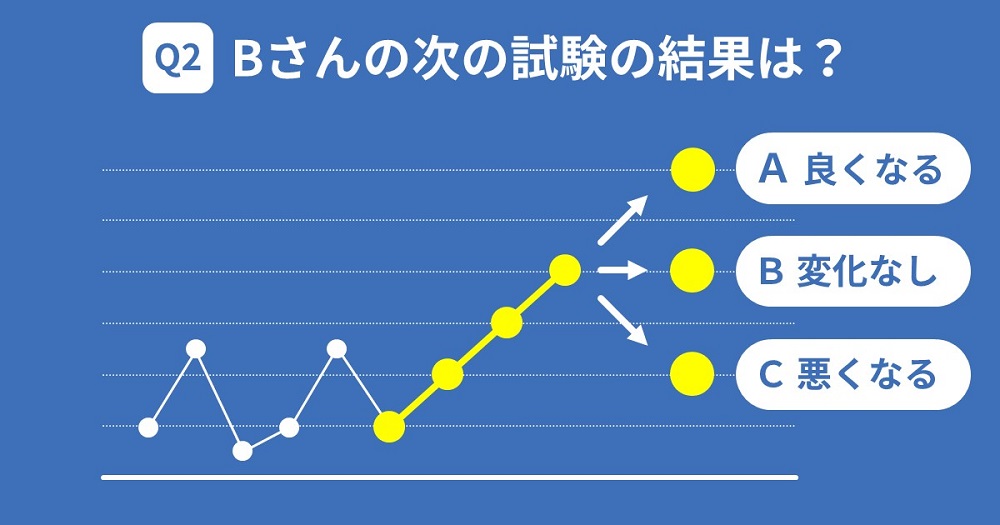
「Bさんのこれまでの努力がここに来て実を結んだのだ」とさらに良くなることを期待する方もいれば、「そろそろ落ち着く頃合いだ」と考えて「変化なし」を選ぶ方もいるでしょう。少なくとも、自分が手塩にかけて指導している生徒であれば、AかBを選びたくなるのが人情です。

ところが、統計的な知見に基づいて考えるならば、８月の試験結果で最も確率が高いのは「C 悪くなる」です。

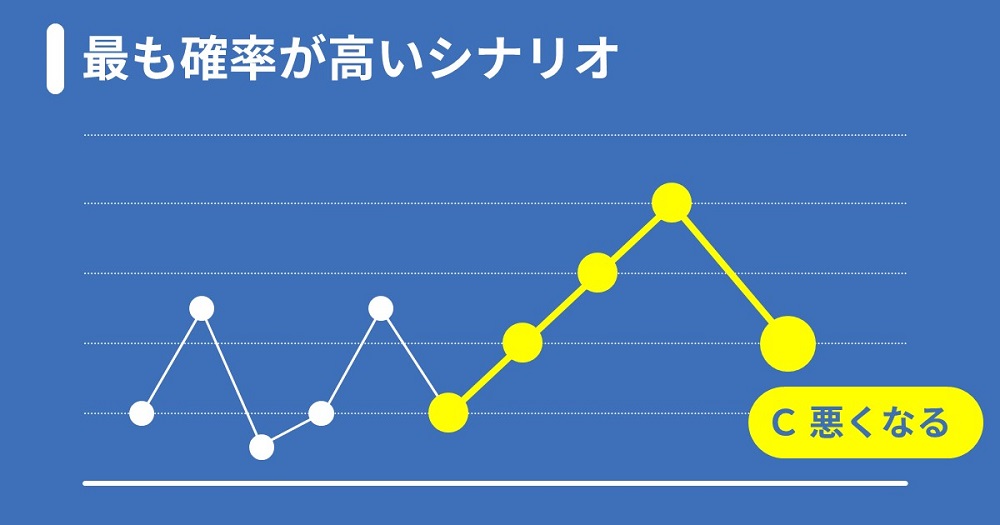
「そう何回も成績アップは続かない」と直感的にCを選んだ方もいらっしゃると思いますが、これは「平均への回帰」という立派な統計的現象の１つです（こちらも詳しく後述します）。

ここまでAさんBさんの２つの例を見てきましたが、みなさんの直感は統計的な結論と比べていかがでしたでしょうか。「なぜそう言えるの？」と疑問を感じた方はぜひ、ここから先の統計の基礎的な考え方を一緒に学んでいきましょう。

データと誤差

ここからは、ここまで見たデータを理解するための統計学の基礎知識を紹介します。前半は「誤差」、後半は「回帰」というテーマを扱います。２つテーマを解説した後、AさんBさんの例に戻って「統計の知識を成績データの読み取りにどう活用するのか？」をお話しますので、お付き合いいただければと思います。

データには必ず誤差が含まれる

はじめに知っていただきたいことは、私たちが手にするあらゆるデータには必ず「誤差（統計誤差）」が含まれているということです。データは、私たちが測定したい何かについて、その真の値をそのまま数値化することはなく、必ず何らかの誤差が含まれた形でしか結果を教えてくれません。

データ（実測値）＝ 真の値 ± 誤差

模試においても同様です。模試の得点や偏差値は生徒の学力を数値化したものではなく、何らかの形で上振れ・下振れした値が出ています。つまり、成績データ（得点や偏差値）は、真の学力に誤差がプラスマイナスされた数字ということです。

成績データ（得点や偏差値）＝ 真の学力 ± 誤差

知っておくべき２つの誤差

誤差には２つの種類があります。

系統誤差（Systematic Error）

特定の原因によって一定の偏りとして生じる誤差
　例：試験会場付近で工事があり、騒音のせいで受験者全体が集中を欠き得点に影響した

偶然誤差（Random Error）

明確な原因がない、測定ごとにランダムに生じる誤差
　例：ヤマを張って丸暗記した内容がたくさん試験に出たため、いい点数が取れた

科学実験であれば系統誤差と偶然誤差の両方からの影響を想定する必要がありますが、今回のテーマである模試や受験においては、（一応のところ）公平性を担保する最大限の努力がなされている前提がありますので、系統誤差のことはあまり考えなくて良いでしょう。生徒の成績データを見る際には、どの程度偶然誤差による影響があったかを見極める必要があります。

成績データにおける偶然誤差の例

• 当日、いつもより体調がよかった
• 当日、いつもより緊張していた
• 適当に埋めた選択肢がまぐれ当たりした
• 苦手な内容が多く出題された
• 直前に読んだ教科書の内容がそのまま出題された
• 試験中に消しゴムを落として時間をロスした

平均への回帰

誤差に次いで重要な内容として「回帰（平均への回帰）」を解説します。

誤差と正規分布

すべてのデータには誤差が含まれますが、誤差（特に偶然誤差）の大きさは正規分布に従うと考えます。正規分布を表す山型のベルカーブは誰でも一度は見たことがあるのではないでしょうか。誤差は±0を頂点に、そこから離れれば離れるほど生じる可能性が小さくなります。

例えば、ある模試の点数において、±10点程度の誤差は80％の確率で生じうるが、それ以上離れて±50点の誤差が生じる可能性は10％未満である、といったイメージです。適当に埋めた5つの選択肢のうち、1～2個が偶然当たることはあっても、５つすべてが当たることは極めて稀だということです。

外れ値の次は平均に近づく

幸運に幸運が重なって、ありえないほど良い結果が出た試験があったとします。例えるならば、定期テストでいつも350点前後の生徒が、偶然（＝偶然誤差）の力だけで450点を取ったというような場合です。誤差は正規分布に従うと考えるならば、およそ100点分の誤差という極めて小さい確率を引き当てたということです。

では、そのあり得ない幸運があった次の試験の“誤差”はどうなるでしょうか。当然、前回を上回る幸運が生じることは考えづらく、現実的には前回よりもずっと小さい誤差を引き当てることになります。結果、得点はいつもの350点前後に落ち着くと予想されます。

このように、極端に良い/悪い結果（＝外れ値）が生じた場合、その次の回は極めて高い確率で過去の平均値に近い値に戻る現象を「平均への回帰」と言います。極端に良い結果の後はそれより悪い結果が生じますし、極端に悪い結果の後はそれより良い結果が生じるということです。

難関校指導のプロ講師が教える成績データの正しい見方

ここからはいよいよ冒頭のAさんBさんの例に戻り、「誤差」と「平均への回帰」という２つの統計知識を使って成績データをどのように読み解くのかを説明していきます。

早速、入塾後に偏差値が53から48に下がってしまったAさんのケースを振り返ってみましょう。冒頭では、偏差値が下がった理由は「誤差の範囲内」であると解説しました。そう結論づける根拠は、「成績データ＝真の学力±誤差」という式にあります。

Aさんの真の学力を言い当てることは困難ですが、過去の模試の平均偏差値を使うことである程度代用できます。グラフに記載のある値から、過去の偏差値の平均は50.8と計算できます。これがAさんの真の学力だと仮定するならば、直近の模試の偏差値48は「50.8－2.8」、つまり、真の学力から2.8ほど低い偏差値であったと言えます。

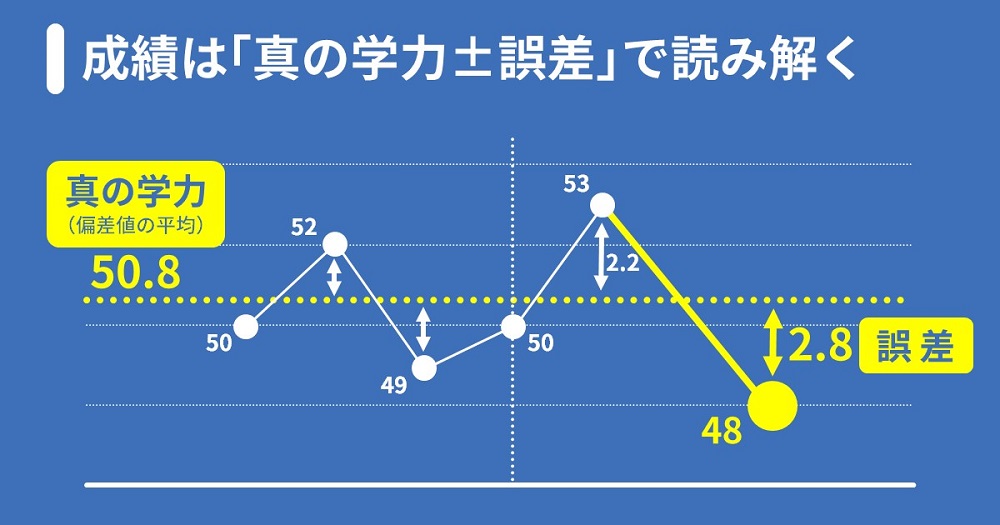
みなさんの実感に照らして考えていただきたいのですが、偏差値３程度の上下は日常茶飯事と言えるのではないでしょうか。53から48というところだけを見ると、一気に偏差値が５も下がった様に見えます。ところが統計的な観点からは、偏差値53は真の学力から2.2の上振れ、偏差値48は真の学力から2.8の下振れで、いずれもよくある範囲の変動です。

「成績データ＝真の学力±誤差」という視点で見ることで、「今回は模試の結果が悪かった」というときであっても、冷静に結果を分析することができるようになります。

同様に、Bさんの例を見てみましょう。まったく同じ考え方で計算すると、仮説としてBさんの真の学力は偏差値49.8。その場合、直近の偏差値は54で、誤差4.2は過去最大の値です。

偏差値で4.2というのは、ありえなくはありませんが、誤差と考えると少し大きい値です。この次の模試は平均への回帰が生じ、偏差値54よりは小さな値になるだろうと考えるのが統計的な発想です。

「成績データ＝真の学力±誤差」という視点で見ると、AさんやBさんのグラフの読み解き方も変わってくるのではないでしょうか。

近似直線で学力の伸びを測る

ここまでが統計の基礎中の基礎ですが、ここで一度「真の学力自体が右肩上がりで伸びているのでは？」という可能性を考えてみましょう。実際、真の学力を伸ばすのが学習塾のミッションですので、模試の結果が右肩上がりで推移した場合には、思惑通り学力も向上していると考えたくなります。

Bさんのケースでは、「入塾以来、コツコツと勉強を頑張ってきたBさん」という説明がありますので、中長期的に学力が伸びてきたと仮定しましょう。この場合、近似直線を取ると伸びの様子を可視化することができます。

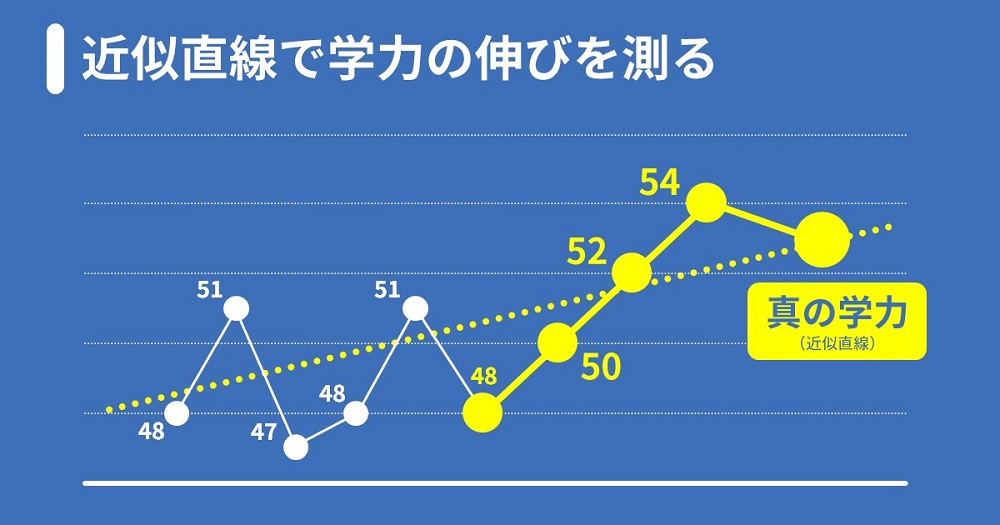
近似直線はエクセルのグラフ作成機能で簡単に作ることができます。

Bさんの努力により継続的に学力が向上している場合、過去の平均値をとるよりも近似直線をとった方が、真の学力をより正確に表していると考えられます。また、統計的には、直線と各データの距離の総和が最小になるように計算する「最小二乗法」によって算出します。

真の学力を見極めて生徒を成功に導こう

Bさんの例では、真の学力を「平均値」と「近似直線」の２つの方法でグラフ化しました。ここで「真の学力を測るにはどちらを使うべきなのか？」という疑問を持たれた方も多いのではないでしょうか。次の模試の偏差値を予測するとき、平均値では49.8、近似直線では53程度が期待値になります。実務レベルでは大きな違いがあります。

結論からいえば、「真の学力を見極めるのが講師の力量。どちらを採用するかは講師の判断による」となります。日々生徒と向き合う中で、「いまBさんは伸びているな」と思えば近似直線を想定しますし、「Bさんに学力の伸びは感じられない」と思えば平均値で結果を予測します。

これは強く意識していただきたいのですが、データは客観的な記録でしかなく、「データから何が言えるか？」は読み解く人間によって異なります。もし、成績が右肩上がりのグラフでも、「本来こんなに得点できる学力はないはずだ」と思うのであれば、「偶然の好成績が複数回繰り返されたにすぎない」と判断すべきなのです。

授業中の受け答えの様子や小テストの正誤傾向、単元ごとの得意不得意やありがちなミスのパターンなど、生徒一人ひとりをしっかりと観察し、受験の合格に向けて今どの程度の学力にあるのかを見極めるのは講師自身です。もちろん、その見極めのために客観的な成績データは欠かせませんが、常にデータは自身の感覚に照らして批判的に見る必要があります。

弊塾では、学習塾のデータ活用を進めることで講師の指導力を高める取り組みを行っています。その一端を紹介した記事もありますので、ぜひあわせて御覧いただければと思います。

5つのデータ活用で塾講師の指導力を育てる！教え方のうまい講師は何が違うか？

以上、統計学の知識を使った成績データの正しい見方について解説しました。きっと成績データの見え方が大きく変わったのではないでしょうか。模試の結果の良し悪しに振り回されることなく、良き指導で多くの生徒を成功に導くことができるよう祈っています。